Issue #89: Encoding Cyclical Features in Time Series

💊 Pill of the Week

When working with time-series data, we often deal with features that have a cyclical nature, such as:

• Hours of the day (0 → 23)

• Days of the week (Monday → Sunday)

• Months of the year (January → December)

• Seasons (Spring → Winter)

• Angles in degrees (0° → 359°)

• Wind directions (0° → 359°)

• Phase measurements (0 → 2π)

A key challenge in encoding these features is that the difference between the last and first values in the cycle should be small. However, naive numerical encodings fail to capture this relationship.

In this article, we will explore why linear encodings fail, how trigonometric transformations solve the problem, and how different models handle cyclical features.

The Pitfall of Linear Encoding

A common mistake is to represent cyclical time features as a single continuous variable. For instance, consider encoding hours as integers:

At first glance, this seems fine, but there are several major flaws:

1. Discontinuity at cycle boundaries:

   • 00:00 and 23:00 are actually one hour apart, but the model sees them as being 23 units apart

   • This same problem occurs with other cyclical features:

     • December (12) and January (1) are adjacent months but appear maximally distant

     • Sunday (7) and Monday (1) are consecutive days but appear far apart

2. False relationships:

   • In our hours example, midnight (00:00) and noon (12:00) appear to have a meaningful numerical relationship, but they don't

   • Similarly, Wednesday (3) appears closer to Monday (1) than to Sunday (7), which doesn't reflect reality

3. Loss of cyclic patterns:

   • Seasonal trends become harder to detect when December and January are at opposite ends of the scale

   • Daily patterns are artificially split at midnight when 23:59 and 00:00 are treated as far apart

This issue occurs with any cyclical feature, whether it’s days of the week (Sunday vs. Monday) or months of the year (December vs. January). The model misinterprets distances between values, leading to suboptimal performance.

Trigonometric Encoding

To encode cyclical features properly, we use sine and cosine transformations:

\(\text{sine} = \sin\left(\frac{2\pi \cdot x}{T}\right)\)

\(\text{cosine} = \cos\left(\frac{2\pi \cdot x}{T}\right)\)

where:

• x is the feature value (e.g., hour of the day).

• T is the period (e.g., 24 for hours, 7 for days of the week).

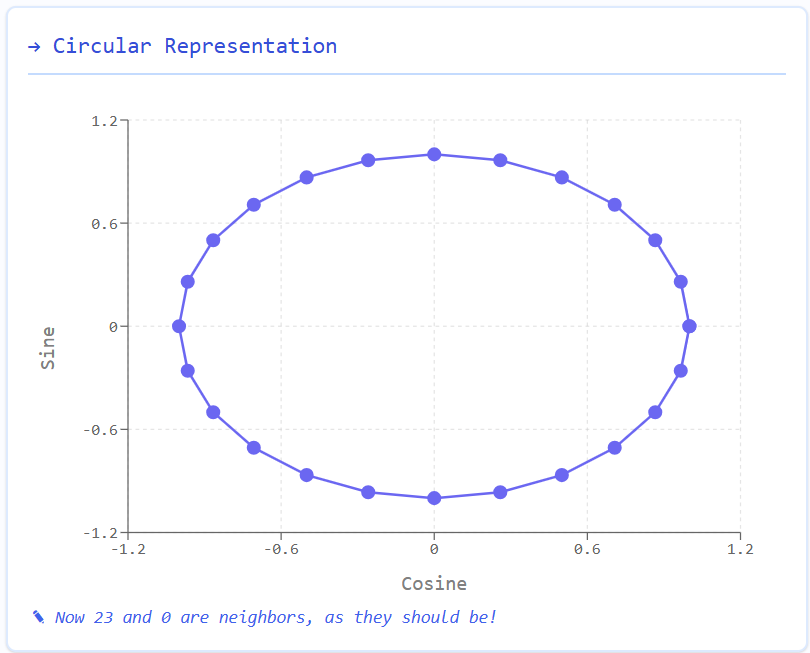
This transformation maps the time values onto a circle, ensuring that adjacent values remain close together while maintaining a unique representation for each time point.

Example: Encoding Hours of the Day

Let’s encode hours into sine and cosine values in Python:

import numpy as np
import pandas as pd

# Create a DataFrame with hours from 0 to 23
df = pd.DataFrame({'hour': np.arange(24)})

# Apply sine and cosine transformations
df['hour_sin'] = np.sin(2 * np.pi * df['hour'] / 24)
df['hour_cos'] = np.cos(2 * np.pi * df['hour'] / 24)

print(df.head())

This generates a table like:

Why Use Both Sine and Cosine?

Using only sine or only cosine would cause duplicate values for different time points.

For example, if we only use cosine:

• 00:00 and 12:00 both get cos(0) = 1.0 and cos(π) = -1.0, meaning they appear identical to the model.

• But 00:00 and 12:00 are very different times!

By combining sine and cosine, we create a two-dimensional representation that uniquely encodes each time point.

Let’s see it visually:

How Different Models Handle Cyclical Features

1. Neural Networks

Neural networks can easily learn complex relationships between sin(x) and cos(x), making cyclical encoding a great choice. Their ability to learn non-linear relationships means they can effectively capture the circular nature of the data.

Implementation Details

import tensorflow as tf

# Custom activation layer for cyclical features
class CyclicalFeatureLayer(tf.keras.layers.Layer):
    def __init__(self):
        super(CyclicalFeatureLayer, self).__init__()
        self.dense_1 = tf.keras.layers.Dense(16)
        self.dense_2 = tf.keras.layers.Dense(2)
    
    def call(self, inputs):
        x = self.dense_1(inputs)
        x = tf.nn.relu(x)
        return self.dense_2(x)

# Example usage in a model
def build_cyclical_model(input_shape):
    model = tf.keras.Sequential([
        tf.keras.layers.Input(shape=input_shape),
        CyclicalFeatureLayer(),
        tf.keras.layers.Dense(64, activation='relu'),
        tf.keras.layers.Dense(1)
    ])
    return model

# Example of how to use it
cyclical_features = ['hour_sin', 'hour_cos', 'month_sin', 'month_cos']
model = build_cyclical_model(len(cyclical_features))

The custom layer helps the model better learn the circular relationships in the data by:

• Processing sine and cosine features together

• Maintaining the relationship between paired features

• Allowing the model to learn optimal circular representations

Do you want to use Neural Networks for Time Series? Revisit this issue:

Issue #36 - Multivariate Time Series models in Keras

2. Tree-Based Models (Random Forest, XGBoost, LightGBM)

Tree models split features one at a time, meaning they may struggle to understand the interaction between sin(x) and cos(x). However:

• XGBoost and LightGBM can learn interactions between sin(x) and cos(x), especially with enough data

• Feature engineering (e.g., manually creating interaction terms) can help trees use cyclical features better

• Deeper trees may be needed to capture cyclical patterns effectively

Implementation Details

def create_interaction_features(df, col_name):
    """
    Create interaction features for tree-based models to better capture cyclical patterns.
    
    Parameters:
    -----------
    df : pandas DataFrame
        DataFrame containing the sine and cosine features
    col_name : str
        Base name of the cyclical feature (e.g., 'hour' for 'hour_sin' and 'hour_cos')
    
    Returns:
    --------
    DataFrame with additional interaction features
    """
    # Multiply sine and cosine components
    df[f'{col_name}_interaction'] = df[f'{col_name}_sin'] * df[f'{col_name}_cos']
    
    # Add squared terms to capture non-linear relationships
    df[f'{col_name}_sin2'] = df[f'{col_name}_sin'] ** 2
    df[f'{col_name}_cos2'] = df[f'{col_name}_cos'] ** 2
    
    return df

# Example usage with XGBoost
import xgboost as xgb

def train_tree_model(df, cyclical_features, target):
    # Create interaction features for each cyclical feature
    for feature in cyclical_features:
        df = create_interaction_features(df, feature)
    
    # Configure model with deeper trees
    params = {
        'max_depth': 8,  # Deeper trees for complex relationships
        'min_child_weight': 5,
        'learning_rate': 0.1
    }
    
    model = xgb.XGBRegressor(**params)
    return model

We discovered XGBoost for Time Series in the past:

Issue #28 - Time Series Forecasting with XGBoost

3. Fourier Series in Facebook Prophet

If you use Facebook Prophet for forecasting, you don't need to manually encode cyclical features! Prophet automatically models seasonality using Fourier transformations, making it a powerful choice for time series with multiple seasonal patterns.

Implementation Details

from fbprophet import Prophet

# Initialize model with custom seasonal components
model = Prophet(
    yearly_seasonality=20,  # Increase Fourier terms for yearly seasonality
    weekly_seasonality=10,  # Custom weekly seasonality
    daily_seasonality=20    # Custom daily seasonality
)

# Add custom seasonal patterns if needed
model.add_seasonality(
    name='custom_pattern',
    period=365.25/2,  # Semi-annual pattern
    fourier_order=5
)

# Fit data
model.fit(df)

# Create future dates for forecasting
future = model.make_future_dataframe(periods=365)

# Make predictions
forecast = model.predict(future)

# Analyze seasonal components
seasonal_components = model.plot_components(forecast)

Prophet's advantages for cyclical features include:

• Automatic handling of multiple seasonal patterns

• Built-in Fourier series transformation

• Ability to handle missing data and outliers

• Automatic detection of changepoints

• Flexible seasonality modeling with adjustable Fourier terms

This makes Prophet a great choice when working with daily, weekly, or yearly seasonality, especially when you have multiple overlapping patterns.

Discover more about Prophet here:

Issue #9: Revolutionize Your Time Series Forecasting with Facebook Prophet

Practical Applications

1. Demand Forecasting

Businesses often track demand by hour, day, or season. Encoding time properly improves forecasting models for:

• E-commerce purchase patterns

• Restaurant foot traffic

• Energy consumption analysis

2. Autonomous Vehicles & Sensor Data

Time-based signals (e.g., temperature changes, light intensity) often repeat cyclically. Proper encoding improves models predicting:

• Traffic patterns

• Weather-dependent sensor data

3. Customer Behavior Analysis

Customers behave cyclically:

• Website traffic peaks at certain times of day.

• Streaming services see spikes on weekends.
  Encoding time correctly helps recommendation systems and marketing models.

Conclusion

Using sine and cosine encoding for cyclical features is a simple but powerful technique that ensures models interpret time-based data correctly. To summarize:

• Avoid naive integer encodings that treat time as linear.

• Use sine and cosine transformations to map time values onto a circle.

• Neural networks handle cyclical encoding well, while tree-based models may need extra tuning.

• Facebook Prophet automatically handles seasonality using Fourier series.

By encoding time correctly, you can significantly improve the accuracy of forecasting, classification, and regression models.

---

‍🎓Further Learning*

Let us present: “From Beginner to Advanced LLM Developer”. This comprehensive course takes you from foundational skills to mastering scalable LLM products through hands-on projects, fine-tuning, RAG, and agent development. Whether you're building a standout portfolio, launching a startup idea, or enhancing enterprise solutions, this program equips you to lead the LLM revolution and thrive in a fast-growing, in-demand field.

Who Is This Course For?

This certification is for software developers, machine learning engineers, data scientists or computer science and AI students to rapidly convert to an LLM Developer role and start building

*Sponsored: by purchasing any of their courses you would also be supporting MLPills.

---

⚡Power-Up Corner

Cyclical encoding is a powerful technique for preserving the natural periodicity of time-based and angular data, but its effectiveness depends on careful validation and optimization. Without proper checks, encoding errors can lead to distorted relationships in your data, reducing model performance.

This section outlines key validation metrics, optimization techniques, and best practices to ensure high-quality cyclical encoding. From continuity and uniqueness checks to performance optimizations, these guidelines will help you implement encoding that is both accurate and efficient.

Let’s dive into the essential validation steps and best practices.